“The data scientists at BigMart have collected 2013 sales data for 1559 products across 10 stores in different cities. Also, certain attributes of each product and store have been defined. The aim is to build a predictive model and find out the sales of each product at a particular store.” - Kaggle

There is a brief overview of the data and variables in figure 1 below. I also encourage taking a look at the notebook I used for this project to get more insights. The link can be found here.

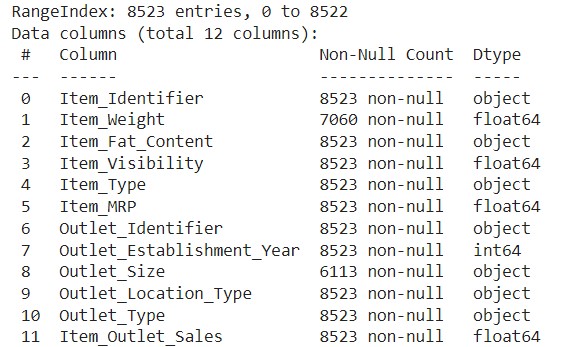
Figure 1 | Overview of the data

Data cleaning and preprocessing

Item_Fat_Content

A count plot showed that there seem to be 5 values for Item_Fat_Content, however we should only have 2, regular or low fat. so I made the Item_Fat_Content a dummy variable such that lowfat is 1, and regular 0.

Nan values

Noted that some items have Nan values for weight, likely an input error so try to correct by looking at similar identifier and filling that in. Left with 4 Nan values where this could not be done, I chose to drop those data points.

The other variable with Nan values is outlet_size. I initially tried using a similar approach as for the item weight but unfortunately 3 of the 10 identifiers have no size (and are thus all Nan). First, I encoded the non-Nan values. There is order, low to high, so I ordinal encoding is most logical in my opinion. I chose 1 for small, 2 for medium, and 3 for large.

So, to fill in the Nan values of this attribute I tried looking at another attribute and filling them in logically. Attributes that make sense to me are the outlet type, or the location type. It seems reasonable that outlet types have specific sizes or that different types of cities (tier 1-3) have differently sized supermarkets. To use those variables the data had to be encoded first, as the types were either groceryStore or supermarket 1-3. I interpreted this as ordinal data, and encoded it accordingly.

Then, I did some cross-tabulation (outlet_size on type and location_type), and this showed that those attributes could help. Given these observations, I used an imputation strategy to fill the Nan values. I chose to impute based on outlet_type because this has a clearer distinction between the missing values. Note that I assumed the relation between outlet_type and size holds for the 3 supermarkets that have no size in a similar way as the ones who do. I would argue that it makes sense to do this as they belong to the same supermarket chain, but another approach here could be possible.

Transforming certain variables

I do not think outlet_establishment_year is a very useful column for a model, the year is quite hard to interpret and has a (much) higher average value than the data from the other variables. Hence, I transformed it to be the age of a store. I did this by subtracting the establishment year from the year of the data (2013).

I also chose to take the log of the Item_MRP, max retail price. The main reason for this is to bring it to a more comparable scale to the other independent variables, making results easier to interpret in a linear model.

Lastly, the independent variable Item_Type has to be encoded. This is nominal data, as categories are not necessarily ordered. I chose for one-hot encoding, despite the dimensionality increase. The main motivation for this was ease of interpretability of results.

Feature selection and new insight

I first did a correlation analysis. The (log) maximum retail price, outlet type, size and item visibility seem to have some correlation with sales. I will only consider those variables, as the other variables have a correlation smaller than |0.1|. Of the variables that are included, log_Item_MRP has the highest correlation, 0.55, with sales.

Then given these features, I split the data into a training and a test set following the 80-20 rule.

After that, a variance inflation factor (VIF) analysis was performed to check for multicollinearity. All VIF scores are below 5 and even close to 1, so multicollinearity is unlikely, and all independent variables can be included.

Unfortunately, as expected, the category of the item did not give much information based on the correlation analysis. However, looking at the item_identifier column each item either starts with FD, NC or DR. Combining this with the category, FD likely means food, NC non-food or other, and DR drink. This provides an easy way to cluster the categories. Hence, I did a one-hot encoding based on food, drink, or non-food. Those variables were included.

Modelling

Linear Regression

The sales data is strictly positive, there are no returns that could lead to ‘negative sales’. Hence, Ordinary Least Squares wouldn’t be appropriate as its estimates would be too small (negatively biased). A truncated regression model could work, but unfortunately the data science packages in Python which I am familiar with do not offer this. Therefore, I chose Eviews to run the regression. The equation that performed best, based on lowest AIC was the following:

log_item_sales = log_item_mrp outlet_size outlet_type item_visibility type_drink type_food type_non_food

With all variables having a p-value (strictly) lower than 5%. The performance on the test set was measured by the root mean squared error (RMSE) and the mean absolute error (MAE), being 0.69 and 0.55 respectively.

Decision Tree Regressor

Although I am not as familiar with this method as with various forms of linear regression, I only used this in one course, I also decided to use a decision tree regressor. My main motivations for this are capturing potential non-linear relationships in the data, something the truncated regression by definition does not do. The other motivation is robustness to outliers.

I did not account for outliers in the data on purpose. In my opinion, handling outliers (properly) is a complex topic. And while there are methods to identify outliers (IQR range or z-score analysis), it is not always correct to remove, transform or impute those values. Sometimes outliers are genuine extreme values that are important to include in the analysis, and I do not know enough about supermarket sales or the foods that are sold at BigMart to correct for them.

The decision tree regressor did much better, its RMSE is 0.52 and the MAE is 0.40. However, this is on the same features I selected for a linear regression and without (hardly) any hyperparameter tuning. The regression’s features had some log transformations, which are not needed for tree based regressors. Hence, the ‘regular’ features were used in the further tuning of the model to check if I can increase the performance further.

Because the dataset is not overly large and computation is thus not expensive, a grid search for the parameters is possible as well as using a recursive feature selection (RFE). The result of the RFE was that only 2 features were optimal, the max retail price and the outlet type. Lastly the grid search resulted in a 0.13 increase in R2, and an MAE and RMSE that are roughly 25% lower.

Learning experience and extensions

This personal project was exciting for multiple reasons. It was very different than anything I did at university. We did have cases but usually with cleaned data. Therefore, the biggest challenge in this project was cleaning and preprocessing the data. Thinking about encoding (efficiently) and solving issues like Nan-values was something that I had not done before and definitely was insightful. In the future, I will most likely spend more time on the modelling part. The regression did poorly, and while the decision tree regressor did better, it certainly is not good enough yet. A random forest or XGboosting could possibly give better results, especially since the tree-based method performed best so far.